Rules for Symbolic Logic in
Elementary Logic, by Benson Mates

BASIC SENTENTIAL CALCULUS (SC) RULES

P, Introduction of Premises
{i} i. P            P
Any SC sentence (a "well formed formula," or WFF) may be entered on a
line.  The premise number is the line number {i}.

MP, Modus Ponens
{n}   i. P -> Q
{m}   j. P
{n+m} k. Q          i,j MP
If a conditional appears on one line (i) and the antecedent of the
conditional appears on another line (j), the consequent of the conditional
may be entered on a new line (k).  The order of lines i and j does not
matter.  Line k inherits the premises numbers {n+m} of line i and line j.

MT, Modus Tollens
{n}   i. -P -> -Q
{m}   j. Q
{n+m} k. P          i,j MT
If a conditional with negations on both antecedent and consequent appears
on one line (i) and the unnegated consequent of the conditional appears on
another line (j), the unnegated antecedent of the conditional may be entered
on a new line (k).  The order of lines i and j does not matter.  Line k
inherits the premise numbers {n+m} of line i and line j.

C, Conditionalization
{n} i. Q
{n} j. P -> Q       i C
A conditional with any well-formed antecedent may be entered on a line (j)
if the consequent appears on an earlier line (i).  Line j inherits the
premise numbers {n} of line i.
  OR:
{m}   i. P
{n+i} j. Q
{n}   k. P -> Q       i,j C
A conditional with any well-formed antecedent may be entered on a line (k)
if the consequent appears on an earlier line (j).  Line k inherits the
premise numbers {n+i} of line j, unless the antecedent appears in an earlier
line (i), in which case the line number i may be removed if it occurs among
the premise numbers of j, reducing {n+i} to {n}.


D, Definitional Interchange
The following equivalent expressions may be exchanged for each other
wherever they occur.  The new line inherits the premise numbers of the
old line:
  (P v Q)   <->  (-P -> Q)
  (P & Q)   <->  -(P -> -Q)
  (P <-> Q) <->  ((P -> Q) & (Q -> P))


STRATEGY FOR USE OF SENTENTIAL CALCULUS RULES

1. CONDITIONAL PROOF

If you want to prove a conditional, assume the antecedent (P).  Using
Conditionalization (C) at the end of the proof then removes the extra
premise and forms the conditional to be proven.  If assuming the antecedent
leaves a conditional still to be proven, then assume the antecedent of that
conditional also.  This procedure can be repeated as many times as necessary
(i.e. recursively).  The proof will end with as many applications of
Conditionalization as the number of Premises that were added by this
strategy.


ADVANCED SENTENTIAL CALCULUS (SC) RULES

TH, Theorem
  i. Th         TH #
Any well formed substitution instance of a Sentential Calculus (SC)
Theorem may be entered on a line (i), with the null set () as premise
number.
  OR:
{n} i. P
{n} j. Q         i TH # [where Th# is of the form (P -> Q)]
If a Theorem is a conditional, the consequent of the Theorem may be
entered on a line (j) if the antecedent occurs on an earlier line (i).
Line j inherits the premise numbers {n} of line i.
  OR:
{n}   i. P
{m}   j. Q
{m+n} k. R       i,j TH # [where Th# is of the form (P -> (Q -> R))]
If a Theorem is a conditional, and its consequent is a conditional, the
consequent of the consequent of the Theorem may be entered on a line (k)
if the antecedent occurs on an earlier line (i) and the antecedent of the
consequent occurs on another earier line (j).  The order of lines i and j
does not matter.  Line k inherits the premise numbers {m+n} of line i and
line j.
  OR, in general:
The theorem rule may telescope any number of applications of Modus Ponens
with theorems that have successive embedded conditionals in consequents and
with the successive antecedents available on previous lines, citing all the
lines and adding their premise numbers.

R, Replacement
{n}  i. P
{n}  j. Q        i R # [where Th# is of the form (P <-> Q), a biconditional]
If a line (i) is or contains a part of a line that is a substitution
instance of one side of a theorem that is a biconditional, it or the part
may be replaced with the corresponding substitution instance of the other
side of the theorem and entered on a new line (j).  Line j inherits the
premise numbers {n} of line i.


STRATEGY FOR USE OF SENTENTIAL CALCULUS RULES

2. INDIRECT PROOF (Reductio ad Absurdum)

Assume the negation of the conclusion (P).  The task then is to derive a
contradiction.  If the contradiction involves the conclusion and its
negation, then the proof ends with an application of Conditionalization (C),
with the conclusion in the consequent, and Clavius (Th 16 or 17), to give
the conclusion, free of the added premise.  If the contradiction does not
involve the conclusion, then the proof ends with an application of Duns
Scotus (Th 8), to give the conclusion, Conditionalization (C), with the
conclusion in the consequent, and Clavius (Th 16 or 17), to give the
conclusion, free of the added premise.

Use Indirect Proof when:

   1.  You don't know what else to do.
   2.  The conclusion is simple -- giving a simple negation to assume.
   3.  There is something immediate or obvious that can be done with
       the new assumption.

Note:  Indirect Proofs are not always simpler or easier than Direct Proofs.
However, Indirect Proof was used quite early by the Greeks to show that
2 was an irrational number and that there was no largest prime number.


QUANTIFIER RULES

US, Universal Specification
{n} i. (x)Fx
{n} j. Fc                i US
The universal quantifier (x) may be dropped and the variable x replaced with
any constant c.  Line j inherits the premise numbers {n} of line i.

EG, Existential Generalization
{n} i. Fc
{n} j. (x)Fx            i EG
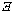The existential quantifier (x) may be added and the constant c replaced with
a variable x.  Line j inherits the premise numbers {n} of line i.

UG, Universal Generalization
{n} i. Fc
{n} j. (x)Fx            i UG
The universal quantifier (x) may be added and the constant c replaced with a
variable x, IF the constant c does not occur in Fx OR in any of the premises
{n} of line i.  Line j inherits the premise numbers {n} of line i.

ES, Existential Specification
{n}   i.     (x)Fx
{j}   j.     Fc             P
{m+j} k.     Q
{m+n} k+1.   Q              i,j,k ES
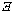If the existential quantifier (x) from a line i is dropped and the variable
x replaced with a constant c as a premise on line j, and Q is derived on
line k with j as a premise, then Q may be entered on line k+1, IF the
constant c does not occur in Q, OR in line i, OR in any premise {m} of line
k.  Line k+1 inherits the premise numbers {m+n} of lines i and k, except
for j.

Q, Quantifier Exchange
The following equivalent expressions may be exchanged for each other
wherever they occur.  The new line inherits the premise numbers of the
old line:
  -(x)Fx  <->  (x)-Fx
   (x)-Fx <-> -(x)Fx
  -(x)-Fx <->  (x)Fx
   (x)Fx  <-> -(x)-Fx



PROPERTIES OF RELATIONS
Symmetrical:    (x)(y)(Rxy -> Ryx)     next to, married to
Asymmetrical:   (x)(y)(Rxy -> -Ryx)    north of, older than
Nonsymmetrical                         loves, brother of

Transitive:   (x)(y)(z)((Rxy & Ryz) -> Rxz)    north of, ancestor of
Intransitive: (x)(y)(z)((Rxy & Ryz) -> -Rxz)   mother of, father of
Nontransitive:                                 loves, different from

Totally Reflexive:   (x)Rxx                        identical to
Reflexive:           (x)((y)(Rxy v Ryx) -> Rxx)   same age as
Irreflexive:         (x)-Rxx                       north of, married to
Nonreflexive:                                      loves, hates, critizes



QED

At the end of a successful proof, the logician or mathematician optionally
can write QED, an abbreviation for the Latin phrase quod erat
demonstrandum, meaning "which was to be proven."  This was a translation
of the Greek phrase hóper édei deîksai, which meant "the very thing it was
needed to show."

Return to Index