It is well-known that many programs, devised in order to insure the clarity of mathematical concepts, as well as to secure the foundations of mathematics, 
have resorted to imposing restrictions on the methods of reasoning usually permitted in the formulation of mathematical statements and proofs. From the standpoint of consistency, it is hoped that the kinds of reasoning which lead to paradox can be disallowed. Hence mathematics would be saved from the fear of paradox by the security of its methods. From the standpoint of clarity, regulations were imposed which required that the concepts of mathematics adhere to stringent requirements of exactness and perspicuity, often formulated in terms of psychological criteria. Hence a theorem of mathematics would be completely understood, rather than merely accepted because no fault could be found with its proof. If by mathematics one understands the usual content of Algebra, Geometry, and Analysis, it is found that each attempt to restrict the usual methods invariably creates restrictions which are so severe that an adequate development of these disciplines is not possible within the confines of the restrictions imposed. Where it was hoped that subjecting mathematics to restricted methods would cause the unclear concepts and paradoxes to precipitate, leaving a transparent, consistent mathematics in its purest form, it was found that too much of mathematics was lost as well in the process.
Gödel has defended classical mathematics against each of the major programs of restricted methods. He has rejected intuitionism, semi-intuitionism, the vicious circle principle, and constructive or finitist programs in general.
Gödel argues forcefully that the concepts of classical mthematics are indeed understood and are "sufficiently clear for us to be able to recognize their soundness...."[1] Whether a mathematical concept is ever "completely given in mathematical intuition" or not does not seem to be a resolvable issue. But Gödel contends that the concepts of classical mathematics, including those involving the transfinite, are meaningful, can be formulated in a manner which is in general satisfactory, and perhaps are as well understood as those allowed by less permissive methodologies. The standard of precision achieved by classical mathematics is usually adequate. Whenever problems arise, "a more profound analysis" is attempted.
Furthemore, Gödel is opposed to applying restrictions intended to ward off paradoxes. Part of his opposition is based on his distinction between logic and epistemology vis à vis mathematics. He argues that the paradoxes of antiquity as well as those discovered in the last hundred years are deceptively mathematical in nature, i.e. they seem to be paradoxes of mathematics when in fact they are paradoxes of logic and epistemology. He shows that the entities of classical mathematics, integers, sets of integers, etc., are rather well-behaved, and no legitimate paradox has been found which involves these and only these entities. Rather, the paradoxes, from Zeno to Cantor and Russell, involve entities which are not strictly speaking part of classical mathematics. Thus in the following passage, discussing Russell's contributions to mathematical logic, the word 'logical' cannot be replaced by 'mathematical'. Gödel states:
I pass now to the most important of Russell's investigations in the field of the analysis of the concepts of formal logic, namely those concerning the logical paradoxes and their solution. By analyzing the paradoxes to which Cantor's set theory had led, he freed them from all mathematical technicalities, thus bringing to light the amazing fact that our logical intuitions (i.e., intuitions concerning such notions as: truth, concept, being, class, etc.) are self-contradictory. He then investigated where and how these common-sense assumptions of logic are to be corrected....[2]
Note that it is our "logical intuitions," those concerning "truth, concept, being, class, etc." which are "self-contradictory." And they are self-contradictory because our "common-sense assumptions of logic" break down. On the other hand, within the domain of classical mathematics, Gödel argues:
It might seem at first that the set-theoretical paradoxes would doom to failure such an undertaking, but closer examination shows that they cause no trouble at all. They are a very serious problem, not for mathematics, however, but rather for logic and epistemology. As far as sets occur in mathematics (at least in the mathematics of today, including all of Cantor's set theory), they are sets of integers, or of rational numbers, (i.e., of pairs of integers), or of real numbers (i.e., sets of rational numbers), or of functions of real numbers (i.e., of sets of pairs of real numbers), etc. When theorems about all sets (or the existence of sets in general) are asserted, they can always be interpreted without any difficulty to mean that they hold for sets of integers as well as for sets of sets of integers, etc. (respectively, that there either exist sets of integers, or sets of sets of integers, or... etc., which have the asserted property). This concept of set, however, according to which a set is something obtainable from the integers (or some other well-defined objects) by iterated application of the operation 'set of', not something obtained by dividing the totality of all existing things into two categories, has never led to any antinomy whatsoever; that is, the perfectly 'naive' and uncritical working with this concept of set has so far proved completely self-consistent.[3]
Moreover, he indicates that Cantor's set theory is a "natural generalization of classical mathematics."[4] Hence the paradoxes, e.g. "something obtained by dividing the totality of all existing things into two categories," do not deal with mathematical entities.
This aspect of Gödel's defense may be summarized as follows:
(i) In thinking that the paradoxes were devastating mathematics, various restrictions on the usual methods of mathematical reasoning were imposed.
(ii) No paradox has been discovered which Involves entities which are strictly speaking mathematicsal: the "set of all sets," the "greatest ordinal number," "sets which are elements of themselves," etc. are logical and epistemological entities which do not belong to classical mathematics proper.
(iii) The concepts of classical mathematics are meaningful, precise, and are capable of being understood because they meet standards of clarity and exactitude which are adequate for their purpose.
(iv) Hence, there is no justification for applying unnecessary restrictions to classical mathematics.
2.) The Vicious Circle Principle.
The search for a once-and-for-all solution to the paradoxes led Russell, Poincaré, and others to the observation that each of the paradoxes trades on a vicious circle in defining an entity which ultimately creates the paradox. Questions of circularity are as old as philosophy., but it was never realized how deeply they could permeate logic and mathematics. Indeed Gödel himself remarked that "any epistemological paradox" could have been employed to yield an undecidable statement of arithmetic.[5],[6] Of course many nontechnical works on logic warn us about circular definitions.
In axiomatic set theory, one of the legislative functions of the axioms is to prohibit the existence of sets which would cause trouble, and the various axiom systems can be classified according to the mamer in which the paradoxes are blocked.[7] If one however wishes to derive totally his mathematics from his logic, it is found that the process of Dedekind Cuts, the fundamental method of establishing the real number system, is badly in violation of the vicious circle principles.[8] Hermann Weyl attempted a development of analysis in Das Kontinuum which adhered to the vicious circle principle, but he was unable to obtain the whole of classical analysis. Recent research [9] has shown that more can be squeezed out of these restrictions than had been expected:
We do not wish to quibble over the meaning of "mathematically interesting." However, "it is shown that the arithmetical statement expressing the consistency of predicative analysis is provable by impredicative means." Thus it can be proved conclusively that restricting mathematics to predicative methods does in fact eliminate a substantial portion of classical mathematics.[11]
Gödel has offered a rather complex analysis of the vicious circle principle and its devastating effects on classical mathematics culminating in the conclusion that because it "destroys the derivation of mathematics from logic, effected by Dedekind and Frege, and a good deal of modern mathematics itself" he would "consider this rather as a proof that the vicious circle principle is false than that classical mathematics is false."[12]
The vicious circle principle as usually stated[13] is dissected by Gödel into four forms:
(1) No totality can contain members definable only in terms of this totality.
(2) No totality can contain members involving this totality.
(3) No totality can contain members presupposing this totality.
(4) Nothing defined in terms of a propositional function can be a possible argument of this function.[14]
The core of Gödel's rejection of the vicious circle principle reduces to his rejection of the view that mathematical entities are "constructed by ourselves." We shall see that this argument hinges an the interpretation of 'construction', and on Gödel's faith in the consistency of the axioms of set theory underlying classical analysis.
If we identify constructions with finite processes, it hardly makes sense to speak of constructing the continuum. Nevertheless, this is precisely the terminology employed in many textbooks of Analysis. Granted, the idea of Dedekind Cuts is heuristically related to a construction, but only so in a loose sense, and is confusing if it deludes someone into believing that something is actually being constructed. Mathematics has a propensity for employing physical or "thing" language, and this does have considerable heuristic value because the metaphors chosen are usually clever and appropriate. Examples are easy to find: extension, dense, generate, approach, determine, dominate, countable, metrizable, compact, etc. We speak of the behavior of functions as if they were children.[15] One of the most "physical" expositions of Dedekind Cuts stated that we can use them "to throw all numbers of This text later goes on to show "how the real number system may be constructed" by means of Dedekind Cuts. Clearly, we may conclude that the notion of being "well-determined" is, for classical analysis, a different notion from the predicative one explained in Feferman.[18] This emphasizes Gödel's main conclusion, that within the domain of classical mathematics, the issues are sufficiently clear, well-determined, and are free from the problems that occur, according to Gödel, outside of this domain.
One of the major lessons learned from the paradoxes is that one simply cannot define a set into existence. It is this fact, the realization that a set can be defined but nevertheless empty, which places axiomatic set theory on a sound foundation. While the observation that the paradoxes were created by impredicative definitions is correct, it may be argued that there are innocuous, perfectly clear, impredicative definitions deeply rooted in classical mathematics, and hence the question of paradox is not reducible to the question of predicativity. Gödel's point, that axiomatic set theory has freed itself from all known paradoxes, reinforces the view that axiomatic set theory provides a sound, adequate basis for classical mathematics, including its inherent impredicativity. This does not mean that research in Predicative Analysis is without purpose. Rather it shows that Predicative Analysis (and constructive methods in general) as a branch of mathematics, is concerned more with the theory of computability, than with the question of providing a sound foundation for mathematics. Hence, the solution to a problem in classical mathematics is not necessarily a computable solution. But this just emphasizes Gödel's argument that:
Here the crucial distinction is "knowability." A classical existence proof tells us that something having certain properties exists. Gödel then is distinguishing between the existence of a computable solution, and the existence of a solution to a problem. Perhaps classical mathematics is concerned with "what there is" and leaves the "whereabouts" as problems for Applied Mathematics and Physics.
Dedekind Cuts, as well as other mathematical concepts "defined impredicatively" do not have to be considered as definitions or constructions. The axiomatic method permits us to consider them as characterizations or descriptions:
The axiomatic assumption of the existence of the set of all reals can be justified on other grounds. The fact that there are "gaps" in the rationals does not entail that these "gaps ought to be filled in." If one thinks of a line being continuous, without "gaps," then by the Pythagorean Theorem, there would be "gaps" if all points were rational.[21] Hence the assumption of the line being continuous is essentially the assumption of the existence of all reals.[22] There is no axiomatic justification for defining a set into existence. Unless one assumes the Continuity Axiom, there will be "gaps in the line," and there will not be any way of "filling them in."[23] Gödel justifies the inherent impredicativity in classical mathematics by arguing that it causes no inconsistency or imprecision when restricted to the domain of classical mathematics. The assumption of the existence of the entities found in the paradoxes leads to contradictions, owing to the instability of these entities in the presence of impredicativity. The axiomatic assumption of the existence of "the totality C of real numbers" has "so far proved completely self-consistent."
Gödel is particularly concerned with Dedekind Cuts because of his desire to derive all of classical mathematics from logic. However, he shows that "least class" or "intersection" definitions also violate the first form of the vicious circle principles.[24] These definitions are not only common in classical mathematics, but in contemporary metamathematics as well. For example, the definition of "Recursive" in Undecidable Theories,[25] definitions of the class of terms and formulas in most texts on logic,[26] as well as the "set of deductive consequences"[27] all involve an intersection definition. This is a further indication of mathematicians' refusal to abstain from methods which are, from their standpoint, clear, precise, and easy to deal with, as well as free from paradox.
3.) Gödel's Research in Intuitionistic Mathematics.
We have seen that Gödel is fundamentally at odds with intuitionism. He has argued forcefully against any bridling of the methods of classical mathematics, and in particular, his rejection of the restriction to predicative methods (even if classical logic is employed) is a further indication of his refusal to adhere to any form of constructive methodology, independently of how 'constructive' is understood. Gödel remarked that because "the whole theory of Aleph's greater than Aleph(1) is rejected as meaningless," Brouwer's intuitionism is "utterly destructive in its results."[28] Gödel's meaning of 'intuition', 'general mathematical concepts', and 'sufficiently clear' In the following is patently and irreconcilably different from the meanings assigned by the intuitionists:
Whether intuitionistic mathematics can be formalized or not has proved to be a moot point.[30] There can be no hope of contrasting classical mathematics with intuitionistic mathematics unless the latter can be made reasonably precise. Those who identify precision with formalization are left little choice but to attempt to do so.
Working within the formalization effected by Heyting, Gödel was able to demonstrate that the intuitionistic arithmetic contained the whole of classical arithmetic under an interpretation, differing from the usual one, but nevertheless adequate for the realization that the two arithmetics are equiconsistent. Thus Gödel showed that the intuitionistic arithmetic [31] was not "narrower" than classical arithmetic, and was not safer either. Whereas consistency was not the primary concern of the intuitionists,[32] it might have been believed that because the intuitimistic arithmetic seemed narrower, it was less likely to be contradictory.[33]
Intuitionistic mathematics has provoked the curiosity of many mathematicians whose owm attitudes are not in accord with intuitionist philosophy. Gödel never was an intuitionist. His research in this area was motivated by specific metamathematical considerations, e.g. to determine the relative strengths of the two systems, and this research does not mark an "intuitionistic period" in his development. His interest, however, has proved to be valuable. For example, the Axiom of Constructibility which he employed to prove the consistency of the Continuum Hypothesis with the usual axioms of set theory, has its origin in the iteration principles of Weyl's Das Kantinuum.[34],[35]
4.) Gödel's Dilemma of Higher Axioms.
Whenever the basic concepts of a mathematical discipline are sufficiently clear, questions formulated in terms of these concepts are meaningful, and deserwe to be answered. Assuming the consistency of the basic axiomatic system in question, a statement may be provable, disprovable, or undecidable relative to this axiom system. If a statement turns out to be undecidable, it does not lose its meaning. Instead, its truth or falsehood is determined by evaluating those axiom systems in which it can be proved or disproved. At first sight, this seems to cast an aura of arbitrariness over the otherwise objective, factual view we have of mathematics. Gödel has presented us with a dilemma pointing out the unavoidable need for higher axioms, but has also provided criteria by which these axioms may be evaluated, and hence devalues the accusation of arbitrariness
Gödel's dilemma of higher axioms may be stated as follows: Let S be an undecidable statement of an axiom system A .
Either ( S is meaningless ) or ( S is true ) or ( S is false ) .
We do not wish to maintain that S is meaningless because of the clarity of the concepts which express S .
Hence, ( S is true ) or ( S is false ) .
But S cannot be decided by axiom system A .
Therefore, in order to determine whether ( S is true ) or ( S is false ) , we must adjoin a new set of axioms to A forming an augmented axiom system, say A + B , such that from A + B , we may deduce S , or we may deduce not-S , but not both. The augmented axiom system, A + B , is said to decide[36] S .
Gödel argues that mathematics has always resorted to higher axioms and new methods to resolve open questions. One of his examples concerns number theory. Facts about integers can often only be obtained via the methods of analytic number theory. Thus, the real numbers constitute a higher system than elementary arithmetic. While some elementary proofs have been found for theorems originally proved in analytic number theory, this is not always possible. Gödel will show that in order to obtain the answer to a question demonstrably independent of the usual axioms of a theory, one must resort to the addition of new axioms, not previously part of that theory. Since the bulk of mathematics has been shown by Gödel to be both incomplete and incompletable, Gödel's dilemma is unavoidable. However, there are good grounds for believing that any given set of axioms constitutes only a partial description of the theory as a whole. For example,, one can regard integers as special kinds of real numbers. Hence there is nothing mysterious about analytic number theory obtaining results about integers. The fact that one chooses to work with Peano Arithmetic does not mean that he regards the integers as a separate system, wholly distinct from the reals, but rather, that the choice of Peano's Axioms can be based an grounds of simplicity. Of course, the intuitionists do not share this view. Even granting that the integers are "distinguised" kinds of reals is not enough. Gödel indicates that statements about integers can be proved on the assumption of the axiom of inaccessible numbers.[37] This gives tremendous force to Gödel's belief that there is a more intimate relationship between the higher and lower systems than would appear at the outset. Under this view, one introduces axioms as they are needed, but one is not obligated to stop at Peano Arithmetic, or even classical analysis.
Gödel is advocating a method which reflects the actual practices of mathematics. First, an open problem is attacked "no-holds-barred" to see what kinds of answers can be obtained. Then the problem is viewed from the standpoint of how much one must assume, i.e., what axioms are required, in order to obtain these results. This is a different question from the problem of obtaining a solution via any means whatsoever. Gödel offers a number of good reasons for employing this "cutting down" process after the results have been obtained via the higher axioms. The proof via the higher axioms is usually less complicated than the proof, if there is one, carried out in the lower system. Moreover, it is highly unlikely that the theorems would have been obtained at all, before the higher axioms were considered. Also, new theorems can be formulated which were unknown before the higher axioms were introduced. Thus far, proofs obtained in the lower systems have turned out to be indeed more complicated than in the higher systems as, for example, the highly intricate arguments required to avoid straightforward applications of the axiom of choice.
Nevertheless, it is not inconceivable that a question be decided affirmatively by one (natural) higher axiom, and negatively by another. If the question is in fact independent in the lower system, whether we choose to regard it as true or false comes out in the higher system. We now consider Gödel's suggestions for obtaining a coherent axiomatic foundation for mathematics.
5.) Truth Criteria for Higher Axioms.
Before attempting an explication of Gödel's truth criteria, it must be mentioned that the word 'truth' as employed in this context is intended to be in accord with Gödel's remark that the axioms of set theory "force themselves upon us as being true."[38] One could replace 'true' by 'correct', 'acceptable', 'tenable', 'plausible', or other seemingly neutral terminology. In particular, we can think of an axiom being true if and only if it is satisfied in the principal interpretation of the theory in question.[39] Hence, a mathematician who states that he "believes an axiom to be true" is actually indicating what he considers to be the principal interpretation of the theory. It is hoped that the logistic method allows us to recast ontologically suggestive terminology into a form which is meaningful and acceptable to mathematicians of varying philosophical viewpoints, thus ridding ourselves of the nuisance of fruitless, inconclusive debate. This is especially important in the case of Gödel, whose pronounced realism can be seen to have heuristic value (as in the case of "thing" language describing mathematical entities) even for nominalists and formalists, as well as others who do not find it a tenable ontological position. We have avoided discussing Gödel's realism as much as possible in considering his methodology primarily to show that his methodology, which is crucial, can be accepted without accepting his realism.
Gödel argues that the axioms of set theory, as usually considered today, constitute only a partial description of the whole of mathematics. We certainly do not wish to view mathematics as a completed whole since new results and new methods are constantly being developed. It is necessary then to revise and amend our axiom systems, as well as our methods of reasoning, in order to incorporate new achievements. When we add new axioms to the usual ones, we find that not only are certain issues seemingly related to the new axiom decided by the new axioms, but in addition, many questions in lower systems are decided as well. The example of number theory discussed above is particularly important. The integers are trusted by most philosophical viewpoints. Hence we can expect that mathematicians will be particularly sensitive to number-theoretic consequences of higher axioms.
Gödel calls an axiom a "weak extension" if it "has a model which can be defined and proved to be a model in the original (unextended) system."[40] A strong extension, then, would be an axiom which possesses no inner model. He calls an extension "fruitful" if it yields consequences not otherwise obtainable in the lower system, "sterile" otherwise. A fruitful extension which yields number-theoretic consequences is of importance because these consequences can often be confirmed to a degree by computation up to any given integer. Gödel calls this process a "verification," although 'confirmation' would be better terminology since computations are more closely allied with inductive rather than deductive methods. What is crucial however is the fact that these computations are the most tangible evidence available to us. Indeed, one can doubt Peano's Axioms, but it is unreasonable to doubt calculations, the most basic of mathematical facts.
Gödel distinguishes between "plausible" and "implausible" consequences of an axiom. This is perhaps the weakest aspect of his methodology because one can always object to whatever decision is reached. It is difficult to state precisely why the consequences of an axiom are implausible in terms other than mathematicians tend to regard these consequences as untenable. There is no concrete way to resolve differences of opinion, and mathematicians are not always in agreement, as the history of the subject indicates. Today we are accustomed to irrational numbers, imaginary numbers, continuous functions without derivatives, transcendental numbers, and the actual infinite. However, the remarks made by some mathematicians when these concepts were first introduced are not only humorous, but are indicative of the subjectivity which is possible in mathematics.[41] Gödel however feels that most mathematicians are in agreement because the intuition is objective, not subjective, as the intuitionists believe.[42] Moreover, an axiom might have both plausible and implausible consequences, as the axiom of choice is often regarded.[43] But Gödel argues that mathematics has always progressed in this manner, weighing the plausible against the implausible, and notes that conclusive evidence may take centuries to gather. Critics of Gödel's plausibility criteria may be challenged to produce a more decisive method of evaluation. It appears that a thorough knowledge of a mathematical discipline is the only credential for responsible decision-making, and beyond this it does not seem possible to just list what makes a consequence plausible or implausible, other than the fact that it is so regarded by those deeply embedded in this area of research. The value of Gödel's appeal to higher axioms is now apparent. If there is a question of plausibility which is unresolved, the issue may be decided by an axiom which does have universally acceptable consequences. Thus one arrives at a decision by assenting to an axiom which resolves the issue. The axiom is accepted because its consequences are considered desirable. Admittedly, this proposal has its drawbacks, but it must be regarded as a positive approach to the problem, rather then a dismissal, as Gödel views the intuitionists' rejection of the theory of Alephs.
We can summarize Gödel's truth criteria, although it must be mentioned that this list is not any more complete than mathematics is itself. As new problems arise, new criteria will have to be f cmulated.
(i) A fruitful extension is to be preferred over a sterile extension, provided that the fruitful extension does not create implausible consequences in the lower system.
(ii) An extension which yields theorems about integers, thus confirmable by computation up to any given integer, is to be preferred over an extension which is sterile with respect to number theory.
(iii) The needs of applied mathematics are to be taken into consideration, but the fact that an axiom system is employed in applied mathematics does not mean that it must therefore be employed in pure mathematics, because of the essential differences of the two disciplines.
(iv) A question, shown to be undecidable in a lower system, is to be evaluated with respect to the value of its consequences, the value of its negation's consequences, as well as its relationship to the value of other axioms known to decide it.
The third and fourth criteria require some explanation. In the third, we find that Gödel believes that the needs of physics and other areas where mathematics is applied cannot supply an answer to mathematical questions not related to these disciplines. For example, the higher axioms of infinity do not seem to be directly relevant to physics at present,[44] although it is possible that they may yield results, say in partial differential equations, which would be of value to physicists. The fourth criterion points out the importance of searching for tenable higher axioms to decide open questions otherwise unresolvable. Whether an axiom system admits one and only one principal interpretation, or many principal interpretations depends on the nature of the theory in question. For example, the various geometries seem to be equally acceptable interpretations of those axioms common to each,[45] e.g. "two points determine a line uniquely" holds in each interpretation. In the case of axiomatic set theory, Gödel feels that the principal interpretation is indeed unique:
We shall investigate this view when we discuss Gödel's realism.
6.) Some Concluding Remarks an Gödel's Methodology.
Barring any unforseen catastrophe within the bounds of classical mathematics, one can safely assume that Gödel will patently reject any severe limitation or restrictive modification on the procedures and content of classical mathematics. Indeed the major shortcomings of restrictive methodologies in general revolve around their inability to develop an adequate theory of real numbers. Gödel then, as well as most mathematicians, regards classical analysis as fundamentally embedded in the core of mathematics, and any restrictive principle of reason which inhibits the adequate development of classical analysis is a fortiori pathological. Mathematics for Gödel is boundless, having its beginning in the rudiments of logic, extending up to classical analysis, the higher axioms of infinity, and beyond to bolder, richer but as yet undiscovered theories.
Banach., S. and A. Tarski. "Sur la décomposition des ensembles de points en parties respectivement congruentes," Fundamenta Mathematicae, 1924, 6:244-277.
Borel, E. Éléments de la Théorie des Ensembles (Paris, 1949), pp. 200-239.
----- Note VII "Les paradoxes de l'axiome du choix," Leçons sur la Theorie des Fonctions, 4th ed. (Paris, 1950), pp. 287-291.
----- Chapter 11, Elements of the Theory of Probability, translated by John E. Freund (Englewood Cliffs, 1965), pp. 109-117.
Sierpinski, W. Leçons sur les Nombres Transfinis (Paris, 1928).
----- Chapter VI "The axiom of choice. Controversy about it," Cardinal and Ordinal Numbers (Warsaw, 1958), pp. 88-131.
Suppes, P. Chapter 8, Axiomatic Set Theory (Princeton, 1960), pp. 239-252.
In Section 2, Schlegel employs the Continuum Hypothesis:
In Section 3, "The Cardinality of Atom-Spaces,"[48] there is an intricate cardinality argument which blends physical theory with transfinite arithmetic. Gödel, in the "Supplement to the Second Edition" of "What is Cantor's Continuum Problem?" remarked that a physical interpretation could not decide open questions of set theory, i.e. there was (at the time of his writing) no "physical set theory" although there is a physical geometry:
Gödel himself has performed research in cosmology but we do not know if he has criticized Schlegel's article. It would be remarkable if physicists were able to employ set theory, especially transfinite arithmetic, in their work. Historically, physics has employed much of available mathematics, e.g. classical analysis, probability and statistics, group theory, and geometry, with set theory a notable exception. Such an intimate relationship is not easily explained when one considers the apparent divergence of the experimental nature of physics from the intuition inherent in mathematical thought. Moreover, it would tend to indicate that physical theory may actually depend on mathematical discovery; that the question of whether mathematics is being interpreted in physics or physics is being interpreted in mathematics is not as clear-cut as some who would use physical theory as a criterion of mathematical truth seem to indicate.
Cf. also Schlegel's Completeness In Science (New York, 1967), and the review of it by Edward H. Madden in Philosophy of Science, 1967, 34:386-388.
On Gödel's Philosophy of Mathematics, Chapter II
all mathematically interesting statements about the natural numbers, as well as many analytic statements, which have been obtained by impredicative methods can already be obtained by predicative ones.[10]
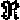into two classes," as if we were crating apples according to size.[16] One of the standard references for Dedekind Cuts, in discussing the paradoxes states:
It seems clear that a statement that refers to itself is not a sensible statement, and so should be excluded from discourse. Also, the members of a class must be themselves well-determined before the class containing them as members can be specified, so that it does not make sense to speak of a class that is a member of itself.[17]
the vicious circle principle in its first form applies only if the entities involved are constructed by ourselves. In this case there must clearly exist a definition (namely the description of the construction) which does not refer to a totality to which the object defined belongs, because the construction of a thing can certainly not be based on a totality of things to which the thing to be constructed itself belongs. If, however, it is a question of objects that exist independently of our constructions, there is nothing in the least absurd in the existence of totalities containing members, which can be described (i.e., uniquely characterized) only by reference to this totality. Such a state of affairs would not even contradict the second form of the vicious circle principle, since one cannot say that an object described by reference to a totality 'involves' this totality, although the description itself does; nor would it contradict the third form, if 'presuppose' means 'presupposed for the existence' not 'for the knowability.'[19]
One can attempt to defend the impredicative definition by interpreting it, not as defining or creating the real number u for the first time (in which interpretation the definition of the totality C of real numbers is circular), but as only a description which singles out the particular number u from an already existing totality C of real numbers. But the same argument can be used to uphold the impredicative definitions in the paradoxes.[20]
For someone who considers mathematical objects to exist independently of our constructions and of our having an intuition of them individually, and who requires only that the general mathematical concepts must be sufficiently clear for us to be able to recognize their soundness and the truth of the axioms concerning them, there exists, I believe, a satisfactory foundation of Cantor's set theory...namely axiomatics of set theory....[29]
...the set-theoretical concepts and theorems describe some well-determined reality, in which Cantor's conjecture must be either true or false.[46]
The next known transfinite number beyond
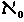is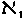 
, or the "power of the continuum." ... The number 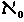is related to 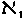by the relation =
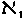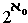.[47]As far as the epistemological situation is concerned, it is to be said that by a proof of undecidability a question loses its meaning only if the system of axioms under consideration is interpreted as a hypothetico-deductive system; i.e. if the meanings of the primitive terms are left undetermined. In geometry, e.g., the question of whether Euclid's fifth postulate is true retains its meaning if the primitive terms are taken in a definite sense, i.e., as referring to the behavior of rigid bodies, rays of light, etc. The situation is set theory is similar, the difference is only that, in geometry, the meaning usually adopted today refers to physics rather than to mathematical intuition and that, therefore, a decision falls outside the range of mathematics. On the other hand, the objects of transfinite set theory...clearly do not belong to the physical world and even their indirect connection with physical experience is very loose (owing primarily to the fact that set-theoretical concepts play only a minor role in the physical theories of today.)[49]
Copyright (c) 1968, 1998 Harold Ravitch, Ph.D. All Rights Reserved